《模型思维:简化世界的人工智能模型》1
模型是客观世界的表示
“Essentially, all models are wrong, but some are useful.” - An Accidental Statistician, George Box
六类人工智能领域的常见问题:
-
权重问题:
TF-IDF模型(Term Frequency - Inverse Document Frequency,词频率-逆文档频率):单一维度
线性回归模型:多维度
PageRank模型:结构权重模型,而非统计权重模型,如网站的链接关系 -
状态问题:
词法分析模型
字符串匹配模型 -
序列问题:
隐马尔可夫模型
最大熵模型 -
表示问题:
向量空间模型
潜在语义分析(LSA)模型
[!NOTE]
如何定义问题的实体?有多少类实体?实体有哪些属性?每一个属性用什么数据类型表示?实体之间又是什么关系?这些就是表示问题要解决的。
- 相似问题(和我在SNA课程中学到的edge的概念有很多相似处)
欧几里得距离:两点之间的直线距离。
曼哈顿距离:城市街区或建筑物之间的行车距离。
切比雪夫距离:际象棋中的距离计算。
闵可夫斯基距离:欧几里得距离、曼哈顿距离、切比雪夫距离的统一。
马哈拉诺比斯距离P:与量纲无关的防维度相关性干扰的距离。
皮尔逊相关系数:两个变量的相关度计算模型。
杰卡德相似系数:两个集合的相似度计算模型。
余弦相似度:两个向量的相似度计算模型。
汉明距离:数据传输错误率的度量模型。
KL散度:两个概率分布的相似性度量模型。
海林格距离:两个概率分布的相似性度量的另一种模型。
编辑距离:一个字符串转换为另一个字符串需要的编辑操作数。
[!NOTE]
各相似模型一般都是由计算相似关系的两个实体的类型来区别的。
- 分类问题:
感知机模型:介绍神经元的概念、感知机的原理、代价函数、梯度下降法、计算示例等。
逻辑回归模型:介绍逻辑回归的应用场景、代价函数、梯度下降法等。
决策树模型:介绍信息熵、ID3算法、C4.5算法、回归树等。
朴素贝叶斯模型:介绍先验概率、后验概率、全概率公式、贝叶斯公式、文本分类示例、拉普拉斯平滑等。
支持向量机模型:介绍肿瘤分类示例、最佳分类面、SVM问题定义、拉格朗日乘子法、数值计算算法等。
[!NOTE]
分类问题是相似问题的应用延展,分类模型一般都基于某一种相似模型。分类的目的都是使类内距离尽量小,类间距离尽量大。
模型之间的关系
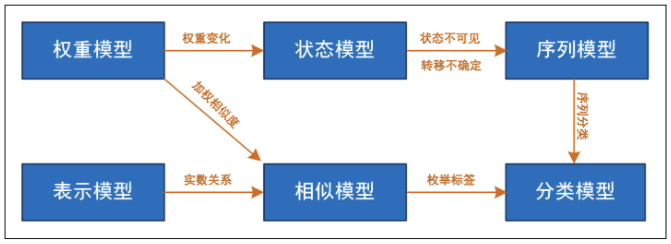
书中 2.9 的部分
如何评价模型的好坏?
- 方法一:
模型的准确率(Precision),表示搜索结果中有多大比例的结果是对的
模型的召回率(Recall),表示正确的结果有多大比例被搜索到了
令一个搜索引擎系统为SE,准确率为P(SE),召回率为R(SE),则有:
$$
F1 = \frac{2\times P(SE) \times R(SE)}{P(SE)+R(SE)}
$$ - 方法二:
模型的表示能力R(m)
模型的简单性S(m)
令衡量这个模型的优劣G(m),则有:
$$
G(m) = \frac{R(m) \times S(m)}{R(m)+S(m)}
$$
模型的运用——知识图谱
整体来说,知识图谱是一个“知识”的网状结构
知识图谱主要包含3个术语:实体(Entity)、属性(Attribute)和关系(Relation)
关系(Relation)在知识图谱中一般用一个三元组(X,R,Y)表示,其中X和Y是两个实体,R是关系
实际实现时,R可以是布尔型,例如夫妻关系可以用是和否的一个布尔型表示;
可以是枚举型,例如用户对书籍的喜爱程度可以用1星、2星、3星、4星、5星等枚举值表示;
还可以是实型,例如用户A和用户B的相似度;也可以是其他可能的类型。
建立知识图谱的流程,以文献计量分析为例:
确定实体的类型:articles, authors, keywords, etc.
确定实体的属性:cited/citing numbers, date, countries, etc.
确定属性的数据类型:number, date, bull, etc.
确定实体间的关系:cited, citing, time series, etc.